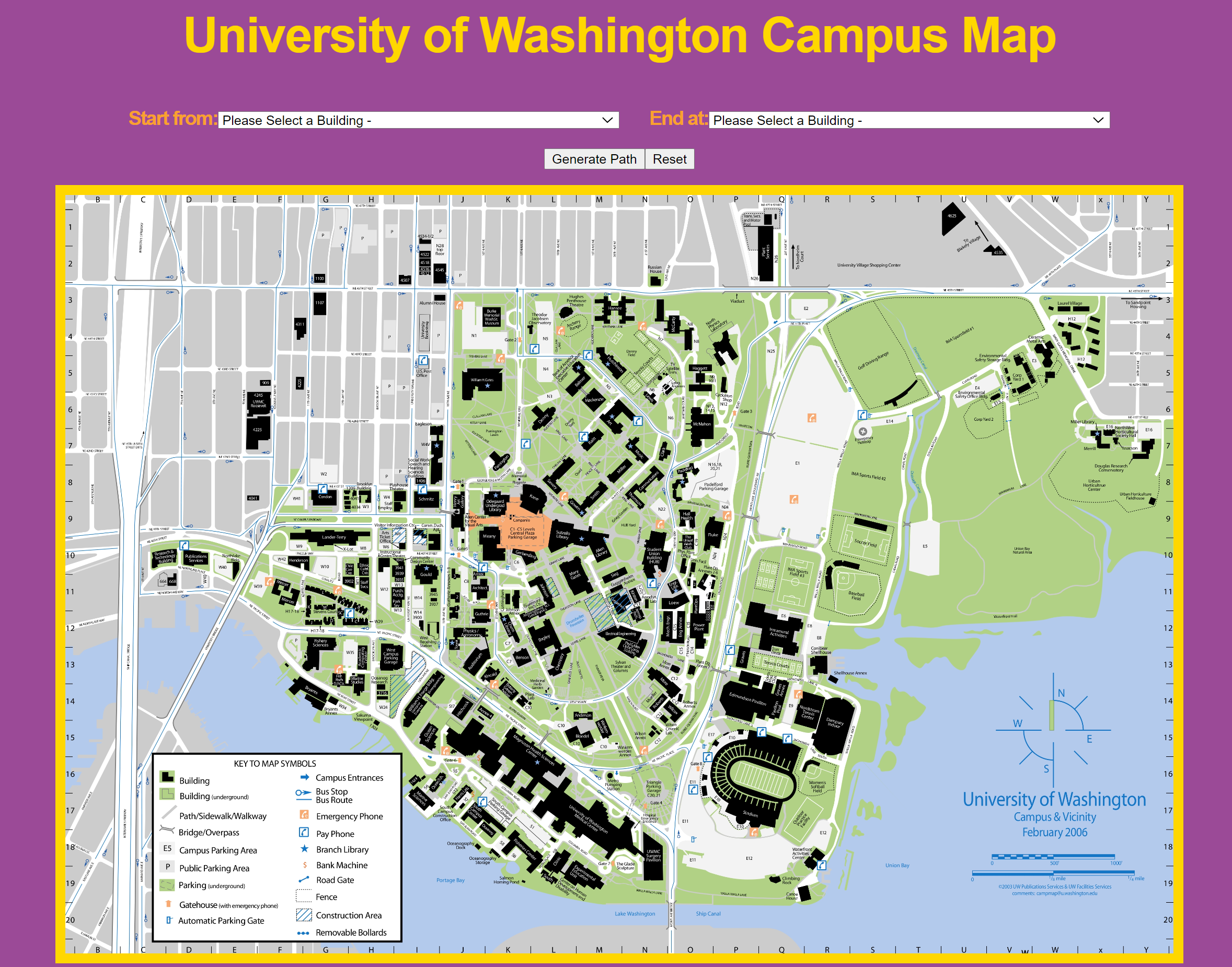
UW Campus Map

Campus Map Project

(request access through email)

Project Overview

UW campus map was made with a variety of modular components each of which were tested with a thorough test suite. These components included a generic graph class, campus map class, back end java spark server, and finally the front end components in react. Each java component includes specification documentation for modularity.

The functionality of this program is rather simple, it allows the user to select two different buildings on campus or near campus. Once the two buildings are selected hitting the generate path button will find the shortest path between those two buildings and draw a line on the map. The reset button will reset all parts of the GUI to their initial state and clear all markings made on the map. The application allows all this while handling bogus inputs from the user so that there are no server errors.

Step 1 - Creating a Generic Graph ADT

DirectedLabeledGraph is an mutable representation of a directed graph made up of generic nodes and generic labeled edges between nodes. Generic graph can be represented as G = (V, E) where V vertices is a set of all the current vertices in the graph G, and E is a list of directed edges currently in the graph.

An edge can be in terms of (p, c, label) where p is the parent vertex pointing to c child vertex, with the edge labeled by label. While the nodes/vertices are represented as a unique value type in the graph.

An edge is invalid if either p or c is not in V or if the label for the edge is not defined, an edge will also have to be unique. So there cannot be two edges (p, c, label) and (p1, c1, label1), where p = p1, c = c1, and label = label1.

An example of a DirectedLabeledGraph would be G(String, String) = (V, E), where V = [A, B, C, D, E, F, G] and E = [(A, B, “Label 1”), (B, G, “Label 2”), (A, E, “Label r”)]

The graph itself is implemented with an adjacency list, with a list of operations that can be done to it. The edge is represented by a private class that includes the start node and the end node.

private HashMap<N, HashSet<Edge>> e;

List of Operations:

addNode(N s)
removeNode(N s)
addEdge(N p, N c, E label)
removeEdge(N p, N c)
removeEdge(N p, N c, E label)
listChildren(N p)
listLabels(N p, N c)
listNodes()
containsNode(N v)
containsEdge(N p, N c, E label)
containsEdge(N p, N c)

Step 2 - Creating the main Campus map Algorithm

Campus map class utilized the generic graph to represent all the coordinates accessible in the map. The vertices in the graph were represented by (x, y) coordinates, while the edges were labeled with the distances between two points if there was a path between them. In the campus map class each building was linked to a unique point, so that you can use building names instead of the coordinates to access locations on the map. Dijkstra’s Algorithm was implemented in order to find the shortest distance between two buildings. The list of buildings, coordinates, and other values were imported with a parser from a csv file.

Generic Dijkstra’s Implementation

public static <T> Path<T> dijkstraPath(DirectedLabeledGraph<T, Double> graph, T s, T d) {
        T start = s; //Starting node
        T dest = d; //Destination node

        // Each element is a path from start to a given node.
        // A path's “priority” in the queue is the total cost of that path.
        // Nodes for which no path is known yet are not in the queue.
        Set<T> finished = new HashSet<T>();
        Path<T> startPath = new Path<>(s);
        PriorityQueue<Path<T>> active = new PriorityQueue<>();
        active.add(startPath);
        while (!active.isEmpty()) {
            // minPath is the lowest-cost path in active and,
            // if minDest isn't already 'finished,' is the
            // minimum-cost path to the node minDest
            Path<T> minPath = active.poll();
            T minDest = minPath.getEnd();

            if (minDest.equals(d)) {
                return minPath;
            }

            if (finished.contains(minDest)) {
                continue;
            }

            List<T> children = graph.listChildren(minDest);
            for (T child : children) { // For all children of minDest
                if (!finished.contains(child)) {
                    // If we don't know the minimum-cost path from start to child,
                    // examine the path we've just found
                    List<Double> costs = graph.listLabels(minDest, child);
                    Collections.sort(costs);
                    Path<T> newPath = minPath.extend(child, costs.get(0));
                    active.add(newPath);
                }
            }
            finished.add(minDest);
        }
        return null;
    }

Step 3 - Developing the Backend Spark Java Server and Front end React GUI

For the react component of the code, an image of the campus map was used where each coordinate point corresponds to the x and y coordinates of the map. Utilizing two threads in the spark java component, I was able to get the list of buildings with their associated coordinates. To allow the clients to select the starting location and destination I used two drop down menus. This made it so no invalid inputs would be given through the client side. The back end returned a list of coordinates for the shortest path which was used to dynamically update the webpage with a path in the image.

Sources

Zatloukal , Kevin. “Campus Maps.” CSE 331 - HW Campus Paths, University of Washington, courses.cs.washington.edu/courses/cse331/20sp/hws/hw9/hw-campuspaths.html.